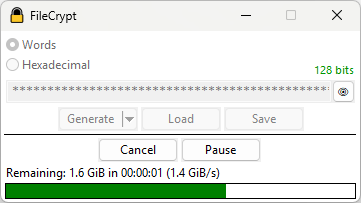
Stream encryption utility

Performs authenticated encryption of streams using Xoofff

Sector-level disk encryption

Windows KMDF and FreeBSD GEOM kernel drivers that provide sector-level disk encryption

Virtual private network

Simple yet effective VPN client and server

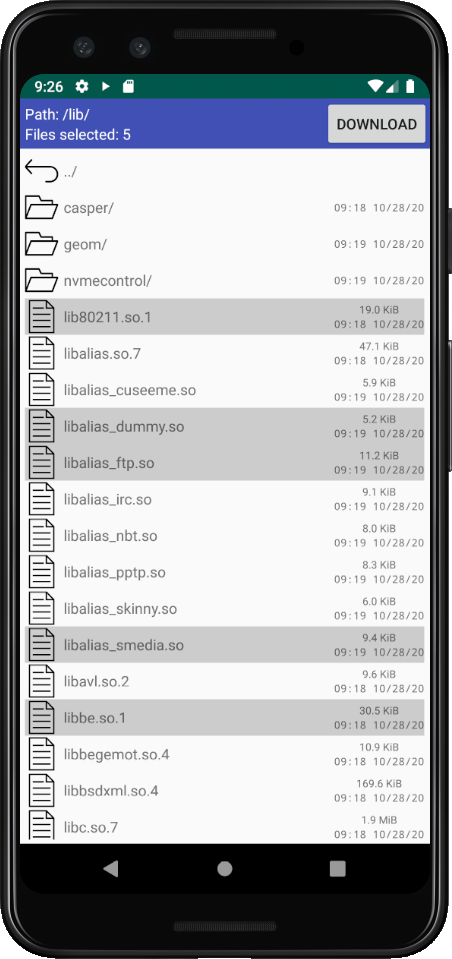
File transfer protocol

Highly secure and efficient file transfer protocol

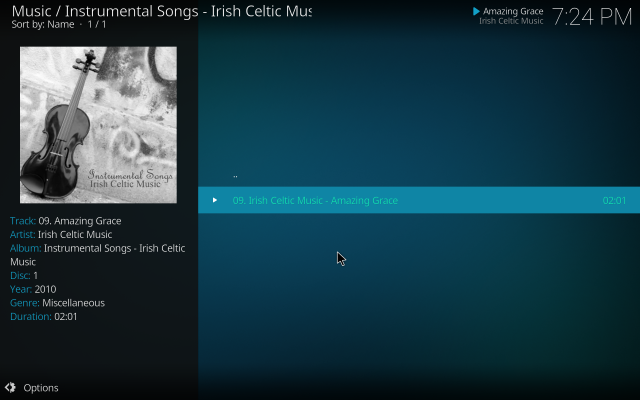
Virtual filesystem add-on for Kodi

Highly secure and efficient virtual filesystem add-on for Kodi

FreeCell for Android

A minimalistic implementation of FreeCell for Android that focuses on correctness

Pythagorean-hodograph curves

Pythagorean-hodograph curves form a remarkable subclass of polynomial curves that have polynomial speed functions, and thus polynomial distance (arc length) functions

Double reflections and rotation minimizing frames

Efficiently and accurately calculates discrete rotation minimizing frames of an arbitrary parametric curve using the double reflection method

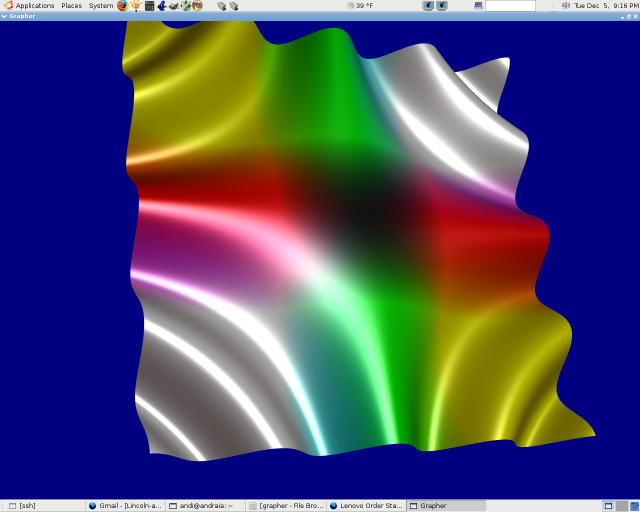
Real-time parametric surface visualizer

Enables the user to visualize arbitrary parametric surfaces in the form <x(s,t), y(s,t), z(s,t)>

Reaction-diffusion simulator

Carries out and visualizes various types of reaction-diffusion simulations

Self-organizing map

Experimentations with self-organizing maps as a way to classify and project high-dimensional data to lower dimensions

Growing neural gas

Visualizes the growing neural gas algorithm in real-time

Cellular automaton

Experimentation with cellular automaton (CA) and compute shaders

Boggle solver

Uses a DAWG data structure to quickly enumerate all solutions given an arbitrary Boggle board

Scrabble solver

Uses a clever graph data structure (GADDAG) to quickly enumerate all solutions given an arbitrary Scrabble board, rack and dictionary

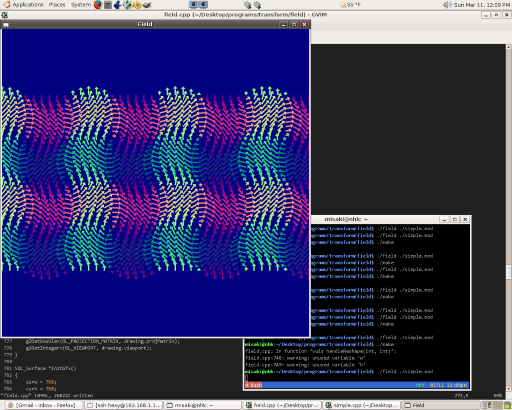
Vector field visualizer

Calculates and renders a real-time visualization of a vector field given an arbitrary parametric function

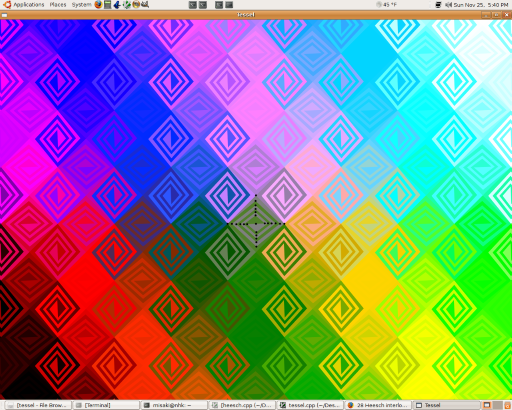
Tessellation

Given an arbitrary shape, various types of tessellations can be realized

Klondike solitaire

My very first endeavor into the world of graphics APIs

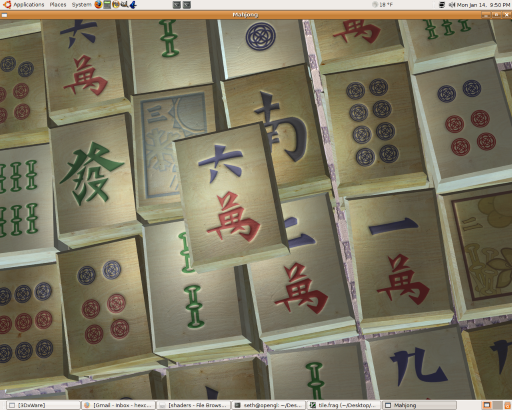
Mahjong solitaire

My take on Mahjong solitaire, complete with a map editor

Procedural jigsaw

A simple jigsaw game, but with code to dynamically and randomly generate the jigsaw pieces